Kernel Initializers

S.No	Lesson Title
1	Introduction
2	Kernel Initializers (K.I.)
3	Need of K.I.
4	Different types of K.I.
5	Keras implementation of K.I.
6	Conclusion

Introduction

Neural networks are gaining popularity in recent days. With this increasing popularity comes the need to have a deeper understanding of how these networks work. One of the most crucial aspects of understanding neural networks is to understand the functionality of weights in a neural network. In layman's terms, neural networks carry all the information about our data through the network, and the updates were done to them throughout the training helps them in carrying more information efficiently. But the most important question that is usually overlooked is how to initialize out weights at the start of our training?

In this article, we'll discuss how weights are initialized and what are the different techniques used to initialize them. We'll also look at how to initialize weights using the Keras library.

Kernel Initializers (K.I.)

We have discussed initializing weights for our neural network architecture in the previous section and this task is done usually with the help of kernel initializers. Kernel Initializers are also known as weight initializers as their main task is to initialize the weights of a neural network. K.I. basically uses a set of predefined statistical distributions or functions to initialize weights. But how?

For example, you can use a normal distribution provided as a part of any K.I. module to initialize weights. In order to use normal distribution hyperparameters such as mean and variance should be provided. Tuning these hyperparameters can lead to effective initialization of weights.

Still, confused about the term "Kernel"? The name was picked from a classical algorithm called SVM. The idea used in SVM's kernels is that the data is transformed from one input space to another space with the help of kernel functions. Neural network layers can be thought of as non-linear terms doing this transformation, that's why the term kernel. But why do we need to initialize weights? Can't we use a constant set of pre-defined weights everywhere? Give a thought to this and then try to see if your ideas match with what is discussed in the upcoming section.

Need of K.I.

The right method of initialization of weights of a neural network plays an important role in improving the overall performance of the model. For example, if all the weights are initialized with a value zero then during each training pass all the neurons will keep on learning the same features leading to very poor performance of the model. This happens because all the neurons become identical in the sense that they have the same weights and same input leading to similar weights updates to each neuron's weight throughout the training process.

There's another major problem which K.I.'s can tackle to some extent. This is known as exploding and vanishing gradients. It can be shown that for deep neural networks as we update weights and move towards the starting layers the weights either get amplified or minimized. For example, if we use large initializations of weights then it might lead to an exponential increase in weights (if we use linear activation functions). This can be shown using the example given below (assume all activations (a) are linear, W represents weight vector, y is the output, x is the input, L is the number of layers):

Ŷ = a ^[L] = W ^[L]W ^[L-1] W ^[L-2].....W ^[2]W ^[1]x

Here Ŷ is the output of our neural network which can be written in the form shown above if we have linear activation. Also, the input vector has only two features, all layers from [1] to [L-1] have also had two neurons implying all the W matrices are of dimension (2,2). Also, assume that W^[L] = W^[L-1] = W^[L-2]=........=W^[2]W^[1] =W. This implies that the output prediction can be written as Ŷ= W^[L]W^L-1x.

You can easily verify that repeated multiplications of W will lead to very large values of a[L]. When this activation is used to update weights during backpropagation it'll lead to an explosion of gradients. This will lead to the cost oscillating around its minimum value.

Another issue is vanishing gradients which can happen when the initialized weights are too small. This will lead to the activation value being too small and then these activation values will lead to smaller weights while doing updates during the backpropagation stage. This implies that the initial layers will learn very few features from the input affecting the overall performance of the model.

Different Types of K.I.

There are different types of kernel initializers and in this article, we'll talk about the ones that are provided specifically by keras. Before discussing about them let's talk about some thumb rules we will stick to:

1. The mean of the activations should be zero.
2. The variance of the activations should stay the same across every layer.

Under the two assumptions stated above the backpropagation, the gradient should not be multiplied by values that are too small or large. It should travel to the initial layer while facing the issue of explosion or reduction. Mathematically we would like the following to hold:

E[a^[l-1]] = E[a^[l]]

Var[a^[l-1]] = Var[a^[l]]

The recommended initialization method that follows these assumptions is Xavier initialization given as follows:

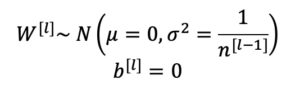
In simpler words, the weights of all the layers are randomly picked from a normal distribution whose mean and variance are given above. Variance is inversely proportional to the total number of neurons in l-1 hidden layers. All the bias terms are initialized with zeros. There are many versions of Xavier initialization which are also labeled as Xavier so don't get confused if you see a slightly different formula at some other place, the idea remains the same.

Now we'll discuss three different types of kernel initializer which are commonly used while working with keras. Before doing that we need to discuss what fan-in and fan-out mean. Take any hidden in the middle of a neural net having a large number of layers. Now the number of neurons in the previous layer is labeled as fan-in and the number of neurons in the next layer is fan-out. Let's discuss about them:

1. Uniform distribution initializer - It uses a uniform distribution given below:

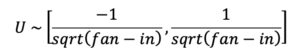
2. Xavier(Glorot) - Keras provides two different types of weight initializers using this technique which are given below:

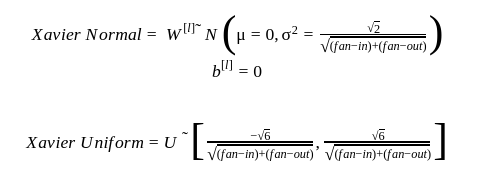
3. HE initializer - This technique is used with the ReLU activation function and gives superior results when compared to glorot initializer. Following distribution was proposed for this technique:

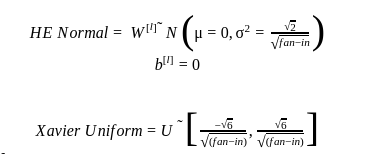
Keras Implementation of K.I.

Let's have a look at how keras can be used to implement the kernel initialize methods with a single layer of our model:

    # Usage in a Keras layer:  
    initializer = tf.keras.initializers.RandomUniform(minval=0., maxval=1.)
    layer = tf.keras.layers.Dense(3, kernel_initializer=initializer)
    
    # Usage in a Keras layer:  
    initializer = tf.keras.initializers.GlorotNormal()
    layer = tf.keras.layers.Dense(3, kernel_initializer=initializer)
    
    # Usage in a Keras layer:  
    initializer = tf.keras.initializers.GlorotUniform()
    layer = tf.keras.layers.Dense(3, kernel_initializer=initializer)
    
    #Usage in Keras Layer:
    initializer = tf.keras.initializer.he_normal
    model.add(Dense(
                16, 
                input_dim=self.state_size, 
                activation="relu", 
                kernel_initializer =initializer))
    

Conclusion

This brings us to the end of the discussion on kernel initializers for neural networks. In this article, we have specifically talked about Kernel Initializers (K.I.'s). 's for Artificial Neural Networks (ANN's) but K.I. 's also played an important role while initializing filter weights for CNN filters or while initializing recurrent weights of RNN's. Though K.I. techniques are overlooked on many occasions after going through this article it would have been clear why these techniques are important. Happy Learning!

References

1. https://keras.io/api/layers/initializers/